External convection (ht.conv_external)¶
- ht.conv_external.Nu_cylinder_Churchill_Bernstein(Re, Pr)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re and Pr, both evaluated at the film temperature. No other wall correction is necessary for this formulation. Method is shown without modification in [2] and many other texts.
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
May underestimate heat transfer in some cases, as it the formula is described in [1] as “appears to provide a lower bound for RePr > 0.4”. An alternate exponent for a smaller range is also presented in [1].
This method applies to both the laminar and turbulent regimes.
References
- 1(1,2)
Churchill, S. W., and M. Bernstein. “A Correlating Equation for Forced Convection From Gases and Liquids to a Circular Cylinder in Crossflow.” Journal of Heat Transfer 99, no. 2 (May 1, 1977): 300-306. doi:10.1115/1.3450685.
- 2(1,2)
Bergman, Theodore L., Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt. Introduction to Heat Transfer. 6E. Hoboken, NJ: Wiley, 2011.
Examples
Example 7.3 in [2], matches.
>>> Nu_cylinder_Churchill_Bernstein(6071, 0.7) 40.63708594124974
- ht.conv_external.Nu_cylinder_Fand(Re, Pr)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re and Pr, both evaluated at the film temperature. No other wall correction is necessary for this formulation. Also shown in [2].
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Developed with test results for water, and Re from 1E4 to 1E5, but also compared with other data in the literature. Claimed validity of Re from 1E-1 to 1E5.
This method applies to both the laminar and turbulent regimes.
References
- 1
Fand, R. M. “Heat Transfer by Forced Convection from a Cylinder to Water in Crossflow.” International Journal of Heat and Mass Transfer 8, no. 7 (July 1, 1965): 995-1010. doi:10.1016/0017-9310(65)90084-0.
- 2
Sanitjai, S., and R. J. Goldstein. “Forced Convection Heat Transfer from a Circular Cylinder in Crossflow to Air and Liquids.” International Journal of Heat and Mass Transfer 47, no. 22 (October 2004): 4795-4805. doi:10.1016/j.ijheatmasstransfer.2004.05.012.
Examples
>>> Nu_cylinder_Fand(6071, 0.7) 45.19984325481126
- ht.conv_external.Nu_cylinder_McAdams(Re, Pr)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re and Pr, both evaluated at the film temperature. No other wall correction is necessary for this formulation. Also shown in [2].
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Developed with very limited test results for water only.
This method applies to both the laminar and turbulent regimes.
References
- 1
McAdams, William Henry. Heat Transmission. 3E. Malabar, Fla: Krieger Pub Co, 1985.
- 2
Fand, R. M. “Heat Transfer by Forced Convection from a Cylinder to Water in Crossflow.” International Journal of Heat and Mass Transfer 8, no. 7 (July 1, 1965): 995-1010. doi:10.1016/0017-9310(65)90084-0.
Examples
>>> Nu_cylinder_McAdams(6071, 0.7) 46.98179235867934
- ht.conv_external.Nu_cylinder_Perkins_Leppert_1962(Re, Pr, mu=None, muw=None)[source]¶
Calculates Nusselt number for crossflow across a single tube as shown in [1] at a specified Re and Pr, both evaluated at the free stream temperature. Recommends a viscosity exponent correction of 0.25, which is applied only if provided. Also shown in [2].
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Considered results with Re from 40 to 1E5, Pr from 1 to 300; and viscosity ratios of 0.25 to 4.
This method applies to both the laminar and turbulent regimes.
References
- 1
Perkins, Jr., H. C., and G. Leppert. “Forced Convection Heat Transfer From a Uniformly Heated Cylinder.” Journal of Heat Transfer 84, no. 3 (August 1, 1962): 257-261. doi:10.1115/1.3684359.
- 2
Sanitjai, S., and R. J. Goldstein. “Forced Convection Heat Transfer from a Circular Cylinder in Crossflow to Air and Liquids.” International Journal of Heat and Mass Transfer 47, no. 22 (October 2004): 4795-4805. doi:10.1016/j.ijheatmasstransfer.2004.05.012.
Examples
>>> Nu_cylinder_Perkins_Leppert_1962(6071, 0.7) 49.97164291175499
- ht.conv_external.Nu_cylinder_Perkins_Leppert_1964(Re, Pr, mu=None, muw=None)[source]¶
Calculates Nusselt number for crossflow across a single tube as shown in [1] at a specified Re and Pr, both evaluated at the free stream temperature. Recommends a viscosity exponent correction of 0.25, which is applied only if provided. Also shown in [2].
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Considers new data since Nu_cylinder_Perkins_Leppert_1962, Re from 2E3 to 1.2E5, Pr from 1 to 7, and surface to bulk temperature differences of 11 to 66.
This method applies to both the laminar and turbulent regimes.
References
- 1
Perkins Jr., H. C., and G. Leppert. “Local Heat-Transfer Coefficients on a Uniformly Heated Cylinder.” International Journal of Heat and Mass Transfer 7, no. 2 (February 1964): 143-158. doi:10.1016/0017-9310(64)90079-1.
- 2
Sanitjai, S., and R. J. Goldstein. “Forced Convection Heat Transfer from a Circular Cylinder in Crossflow to Air and Liquids.” International Journal of Heat and Mass Transfer 47, no. 22 (October 2004): 4795-4805. doi:10.1016/j.ijheatmasstransfer.2004.05.012.
Examples
>>> Nu_cylinder_Perkins_Leppert_1964(6071, 0.7) 53.61767038619986
- ht.conv_external.Nu_cylinder_Sanitjai_Goldstein(Re, Pr)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re and Pr, both evaluated at the film temperature. No other wall correction is necessary for this formulation. Method is the most recent implemented here and believed to be more accurate than other formulations available.
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Developed with test results for water, mixtures of ethylene glycol and water, and air (Pr = 0.7 to 176). Re range from 2E3 to 9E4. Also presents results for local heat transfer coefficients.
This method applies to both the laminar and turbulent regimes.
References
- 1
Sanitjai, S., and R. J. Goldstein. “Forced Convection Heat Transfer from a Circular Cylinder in Crossflow to Air and Liquids.” International Journal of Heat and Mass Transfer 47, no. 22 (October 2004): 4795-4805. doi:10.1016/j.ijheatmasstransfer.2004.05.012.
Examples
>>> Nu_cylinder_Sanitjai_Goldstein(6071, 0.7) 40.38327083519522
- ht.conv_external.Nu_cylinder_Whitaker(Re, Pr, mu=None, muw=None)[source]¶
Calculates Nusselt number for crossflow across a single tube as shown in [1] at a specified Re and Pr, both evaluated at the free stream temperature. Recommends a viscosity exponent correction of 0.25, which is applied only if provided. Also shown in [2].
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
Developed considering data from 1 to 1E5 Re, 0.67 to 300 Pr, and range of viscosity ratios from 0.25 to 5.2. Found experimental data to generally agree with it within 25%.
This method applies to both the laminar and turbulent regimes.
References
- 1
Whitaker, Stephen. “Forced Convection Heat Transfer Correlations for Flow in Pipes, Past Flat Plates, Single Cylinders, Single Spheres, and for Flow in Packed Beds and Tube Bundles.” AIChE Journal 18, no. 2 (March 1, 1972): 361-371. doi:10.1002/aic.690180219.
- 2
Sanitjai, S., and R. J. Goldstein. “Forced Convection Heat Transfer from a Circular Cylinder in Crossflow to Air and Liquids.” International Journal of Heat and Mass Transfer 47, no. 22 (October 2004): 4795-4805. doi:10.1016/j.ijheatmasstransfer.2004.05.012.
Examples
>>> Nu_cylinder_Whitaker(6071, 0.7) 45.94527461589126
- ht.conv_external.Nu_cylinder_Zukauskas(Re, Pr, Prw=None)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re. Method from [1], also shown without modification in [2]. This method applies to both the laminar and turbulent regimes.
- Parameters
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
Notes
If Prandtl number at wall are not provided, the Prandtl number correction is not used and left to an outside function.
n is 0.37 if Pr <= 10; otherwise n is 0.36.
C and m are from the following table. If Re is outside of the ranges shown, the nearest range is used blindly.
Re
C
m
1-40
0.75
0.4
40-1E3
0.51
0.5
1E3-2E5
0.26
0.6
2E5-1E6
0.076
0.7
References
- 1
Zukauskas, A. Heat transfer from tubes in crossflow. In T.F. Irvine, Jr. and J. P. Hartnett, editors, Advances in Heat Transfer, volume 8, pages 93-160. Academic Press, Inc., New York, 1972.
- 2(1,2)
Bergman, Theodore L., Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt. Introduction to Heat Transfer. 6E. Hoboken, NJ: Wiley, 2011.
Examples
Example 7.3 in [2], matches.
>>> Nu_cylinder_Zukauskas(7992, 0.707, 0.69) 50.523612661934386
- ht.conv_external.Nu_external_cylinder(Re, Pr, Prw=None, mu=None, muw=None, Method=None)[source]¶
Calculates Nusselt number for crossflow across a single tube at a specified Re and Pr according to the specified method. Optional parameters are Prw, mu, and muw. This function has eight methods available. The ‘Sanitjai-Goldstein’ method is the default.
The front of the cyliner is normally always in a laminar regime; whereas the back is turbulent. The proportions change with Re; all correlations take this into account. For this heat transfer case, there is no separation between laminar and turbulent methods.
- Parameters
- Re
float Reynolds number of fluid with respect to cylinder diameter, [-]
- Pr
float Prandtl number at either the free stream or wall temperature depending on the method, [-]
- Prw
float,optional Prandtl number at wall temperature, [-]
- mu
float,optional Viscosity of fluid at the free stream temperature [Pa*s]
- muw
float,optional Viscosity of fluid at the wall temperature [Pa*s]
- Re
- Returns
- Nu
float Nusselt number with respect to cylinder diameter, [-]
- Nu
- Other Parameters
- Method
str,optional A string of the function name to use, as in the dictionary conv_external_cylinder_methods.
- Method
Notes
A comparison of the methods for various Prandtl and Reynolds number ranges is plotted below.
(
Source code,png,hires.png,pdf)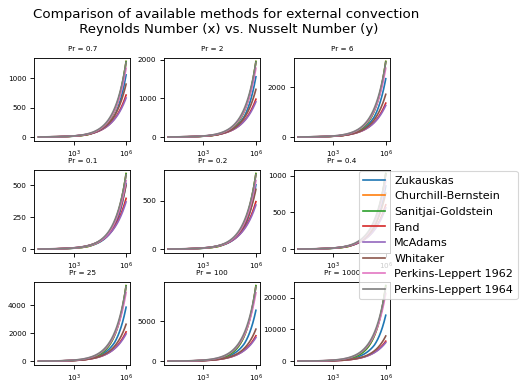
Examples
>>> Nu_external_cylinder(6071, 0.7) 40.38327083519522
- ht.conv_external.Nu_external_cylinder_methods(Re, Pr, Prw=None, mu=None, muw=None, check_ranges=True)[source]¶
This function returns a list of correlation names for forced convection over an external cylinder.
The preferred method ‘Sanitjai-Goldstein’.
- Parameters
- Re
float Reynolds number of fluid with respect to cylinder diameter, [-]
- Pr
float Prandtl number at either the free stream or wall temperature depending on the method, [-]
- Prw
float,optional Prandtl number at wall temperature, [-]
- mu
float,optional Viscosity of fluid at the free stream temperature [Pa*s]
- muw
float,optional Viscosity of fluid at the wall temperature [Pa*s]
- check_rangesbool,
optional Whether or not to return only correlations suitable for the provided data, [-]
- Re
- Returns
Examples
>>> Nu_external_cylinder_methods(0.72, 1E7)[0] 'Sanitjai-Goldstein'
- ht.conv_external.Nu_external_horizontal_plate(Re, Pr, L=None, x=None, Method=None, laminar_method='Baehr', turbulent_method='Schlichting', Re_transition=500000.0)[source]¶
This function calculates the heat transfer coefficient for external forced convection along a horizontal plate.
Requires at a minimum a flow’s Reynolds and Prandtl numbers Re and Pr. L and x are not used by any correlations presently, but are included for future support.
If no correlation’s name is provided as Method, the most accurate applicable correlation is selected.
- Parameters
- Returns
- Nu
float Nusselt number with respect to plate length, [-]
- Nu
- Other Parameters
- Method
str,optional A string of the function name to use, as in the dictionary conv_horizontal_plate_methods
- laminar_method
str,optional The prefered method for laminar flow, [-]
- turbulent_method
str,optional The prefered method for turbulent flow, [-]
- Re_transition
float,optional The transition Reynolds number for laminar changing to turbulent flow, [-]
- Method
Examples
Turbulent example
>>> Nu_external_horizontal_plate(Re=1E7, Pr=.7) 11496.952599969829
- ht.conv_external.Nu_external_horizontal_plate_methods(Re, Pr, L=None, x=None, check_ranges=True)[source]¶
Returns a list of correlation names for calculating Nusselt number for forced convection across a horizontal plate, supporting both laminar and turbulent regimes.
- Parameters
- Re
float Reynolds number with respect to bulk properties and plate length, [-]
- Pr
float Prandtl number with respect to bulk properties, [-]
- L
float,optional Length of horizontal plate, [m]
- x
float,optional Length of horizontal plate for specific calculation distance, [m]
- check_rangesbool,
optional Whether or not to return only correlations suitable for the provided data, [-]
- Re
- Returns
Examples
>>> Nu_external_horizontal_plate_methods(Re=1e7, Pr=.7)[0] 'Schlichting'
- ht.conv_external.Nu_horizontal_plate_laminar_Baehr(Re, Pr)[source]¶
Calculates Nusselt number for laminar flow across an isothermal flat plate at a specified Re and Pr, both evaluated at the bulk temperature. No other wall correction is necessary for this formulation. Four different equations are used for different Prandtl number ranges.
The equation for the common Prandtl number range is also recommended in [2] and [3].
if :
if :
if :
if :
- Parameters
- Returns
- Nu
float Nusselt number with respect to plate length and bulk temperature, [-]
- Nu
Notes
Does not take into account the impact of free convection, which can increase the convection substantially.
References
- 1
Baehr, Hans Dieter, and Karl Stephan. Heat and Mass Transfer. Springer, 2013.
- 2
Bergman, Theodore L., Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt. Introduction to Heat Transfer. 6E. Hoboken, NJ: Wiley, 2011.
- 3
Gesellschaft, V. D. I., ed. VDI Heat Atlas. 2nd ed. 2010 edition. Berlin ; New York: Springer, 2010.
Examples
>>> Nu_horizontal_plate_laminar_Baehr(1e5, 0.7) 186.4378528752262
- ht.conv_external.Nu_horizontal_plate_laminar_Churchill_Ozoe(Re, Pr)[source]¶
Calculates Nusselt number for laminar flow across an isothermal flat plate at a specified Re and Pr, both evaluated at the bulk temperature. No other wall correction is necessary for this formulation. A single equation covers all Prandtl number ranges.
- Parameters
- Returns
- Nu
float Nusselt number with respect to plate length and bulk temperature, [-]
- Nu
Notes
Does not take into account the impact of free convection, which can increase the convection substantially.
References
- 1
Churchill, Stuart W., and Hiroyuki Ozoe. “Correlations for Laminar Forced Convection in Flow Over an Isothermal Flat Plate and in Developing and Fully Developed Flow in an Isothermal Tube.” Journal of Heat Transfer 95, no. 3 (August 1, 1973): 416 https://doi.org/10.1115/1.3450078.
- 2
Bergman, Theodore L., Adrienne S. Lavine, Frank P. Incropera, and David P. DeWitt. Introduction to Heat Transfer. 6E. Hoboken, NJ: Wiley, 2011.
Examples
>>> Nu_horizontal_plate_laminar_Churchill_Ozoe(1e5, 0.7) 183.08600782591418
- ht.conv_external.Nu_horizontal_plate_turbulent_Kreith(Re, Pr)[source]¶
Calculates Nusselt number for turbulent flow across an isothermal flat plate at a specified Re and Pr, both evaluated at the bulk temperature. The formulation of Kreith is used.
- Parameters
- Returns
- Nu
float Nusselt number with respect to plate length and bulk temperature, [-]
- Nu
Notes
Does not take into account the impact of free convection, which can increase the convection substantially. Applies for turbulent flow only.
References
- 1
Kreith, Frank, Raj Manglik, and Mark Bohn. Principles of Heat Transfer. Cengage, 2010.
Examples
>>> Nu_horizontal_plate_turbulent_Kreith(1.03e6, 0.71) 2074.8740070411122
- ht.conv_external.Nu_horizontal_plate_turbulent_Schlichting(Re, Pr)[source]¶
Calculates Nusselt number for turbulent flow across an isothermal flat plate at a specified Re and Pr, both evaluated at the bulk temperature. The formulation of Schlichting is used, which adds a surface friction term to a formulation from Petukhov and Popov.
- Parameters
- Returns
- Nu
float Nusselt number with respect to plate length and bulk temperature, [-]
- Nu
Notes
Does not take into account the impact of free convection, which can increase the convection substantially.
References
- 1
Schlichting, H., and Klaus Gersten. Grenzschicht-Theorie. 9th ed. Berlin Heidelberg: Springer-Verlag, 1997. http://www.springer.com/de/book/9783662075548.
- 2
Gesellschaft, V. D. I., ed. VDI Heat Atlas. 2nd ed. 2010 edition. Berlin ; New York: Springer, 2010.
Examples
>>> Nu_horizontal_plate_turbulent_Schlichting(1e5, 0.7) 309.620048541267